Research Title: An Efficient Resource Allocation Approach based on a Genetic Algorithm for Composite Services in IoT Environments
Research Area: Service resource allocation, Internet of Things, Genetic algorithm
Led by: Min-Hyeop Kim
Summary:
As various types of Internets of Things (IoT) are deployed in a wide range of areas, the need arises to utilize various IoT resources dynamically to accomplish user tasks. We call this environment an urban-scale IoT environment, where various IoT resources that are necessary to accomplish user tasks are directly connected to each other via users’ mobile devices, such as their smart phones. IoT resources are utilized as resources with which to run a composite service that supports user tasks. In this urban-scale IoT environment, it is essential to create efficient binding between a service and an IoT resource so as to execute a composite service for a task successfully. In this paper, we propose a service resource allocation approach which minimizes data transmissions between users’ mobile devices and which effectively deal with the constraints of these types of environments. We transformed the resource allocation problem into a variant of the degree-constrained minimum spanning tree problem and applied a genetic algorithm to reduce the time needed to produce a near-optimal solution. We also defined a fitness function and an encoding scheme to apply the genetic algorithm in an efficient manner. The proposed approach shows a 97% success rate on average when used to find near-optimal solutions, and a linear time growth as the number of IoT resources increases.
Core Approaches:
[Figure 1. Relationship between service gateways and IoT resources]
In this research, we assume that an IoT resource is not able to interact with other resources directly to perform a task. Interaction between resources can be done via service gateways, which are deployed in an IoT environment along with the IoT resources. A service gateway is a computation node that runs service instances. It relays communications between IoT resources to execute a user task. This assumption is made because most IoT resources do not have enough computation power to run service instances. A service instance may require multiple IoT resources to provide its capability, and the service gateways ensure stable connections between necessary IoT resources. If there is an IoT resource that has the networking and computational capabilities to be part of a MANET and to run service instances, we regard it as a service gateway as well. Figure 1 shows the relationship between service gateways and IoT resources. In this IoT environment, IoT resources can be allocated to a gateway to communicate with each other to the extent allowed by the gateway capacity. Gateway capacity refers to the limited number of IoT resources that can be allocated to a gateway simultaneously.
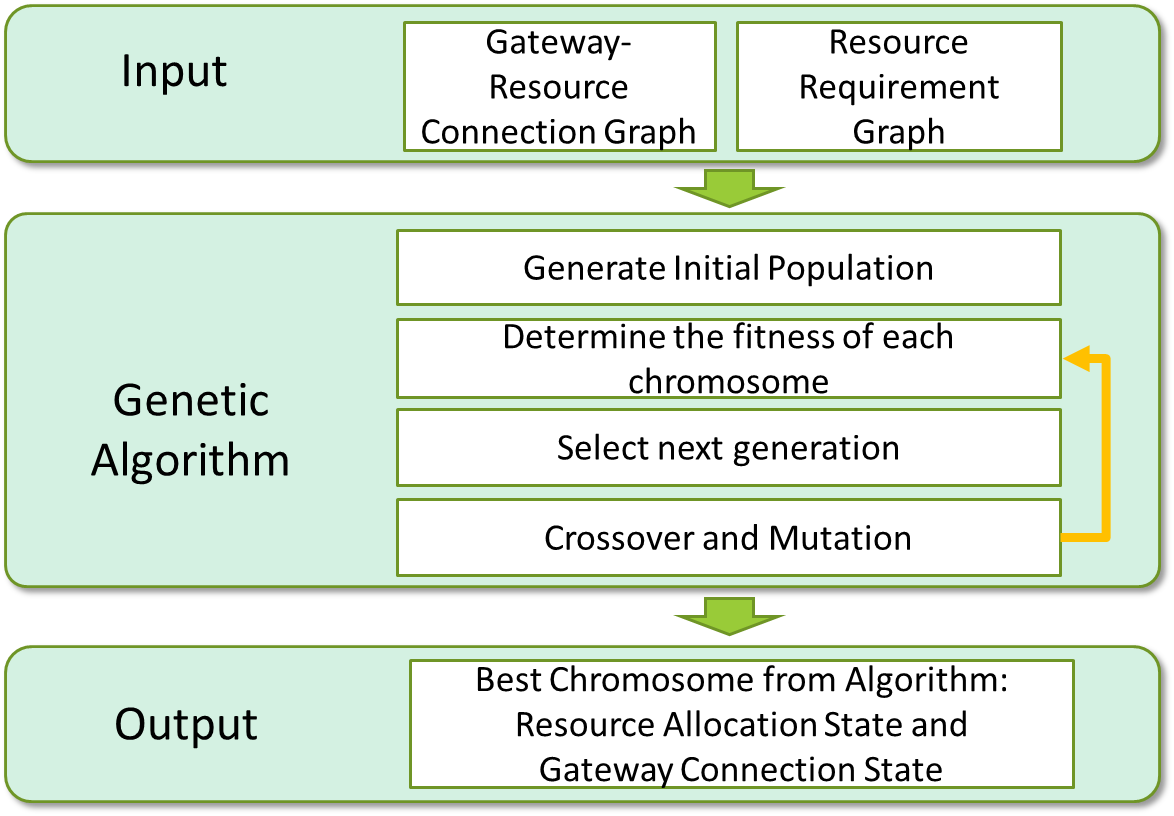
[Figure 2. Overall process of the proposed approach]
Therefore, we propose a service resource allocation method which minimizes the data transmission between service gateways and which effectively deals with the constraints of users’ mobile devices. We transformed the resource allocation problem into a variant of the degree-constrained minimum-spanning tree problem and applied a genetic algorithm to reduce the time required to produce a near-optimal solution. We defined a fitness function and an encoding scheme for the candidate solutions to apply the genetic algorithm in an efficient manner. Figure 2 describes the overall process of the proposed approach.
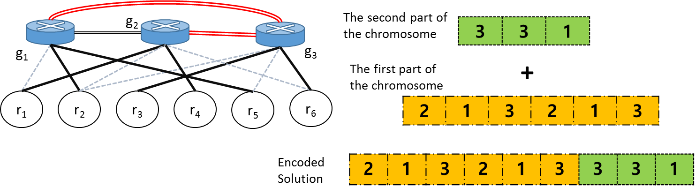
[Figure 3. An example of an encoded solution]
Figure 3 shows an example of the use of the encoding scheme that we propose. The graph on the left is a gateway-resource connection graph given as an input, and the population for the genetic algorithm is generated based on this graph. During the process of the genetic algorithm this population is evaluated by the fitness function, and evolves into generate candidate solutions.
[Figure 4. Fitness function of the resource allocation problem]
The fitness function that we developed is based on the objective function for the DCMST problem which is introduced in earlier work. The objective function of DCMST problem is formulated to minimize the sum of all edge weights in a spanning tree and to impose some penalty on those nodes which violate the degree constraint. We modified this function to formulate our fitness function. The fitness function imposes a penalty when a node violates the degree constraint, and gives more fitness value to a valid connection.
Intermediate Results:
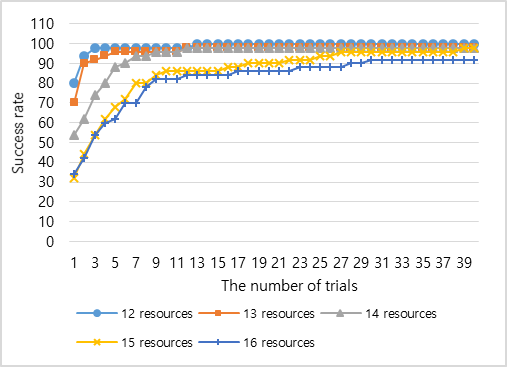
[Figure 5. Success rate change over the number of trials]
We conducted 40 trials for each set of gateway-resource connection graph. If any of the 40 trials generates a near-optimal solution which does not violate any of the capacity constraints, it is considered as a successful case. Therefore, the success rate represents the proportion of the experimental sets that make at least one of the trials successful. Figure 5 shows the changes in the success rate of the proposed approach. As shown in the figure, as the number of trials increases, the success rate also increases. Specifically, the success rate increases rapidly within five trials. If there are more than nine trials, all of the cases show a success rate that exceeds 80%. This means that for a time-critical task, the number of trials can be minimized to reduce the time for resource allocation. In addition, if 40 trials are performed, all five cases show a success rate which exceeds 90%. There were some failures with 13, 14, 15 and 16 IoT resources. However, the maximum success rate of each case is around 98% apart from the case of with 16 IoT resources (in this case, the maximum success rate is 92%). There is a tendency for the success rate of cases with fewer IoT resources to be higher than the success rate of cases with more IoT resources.
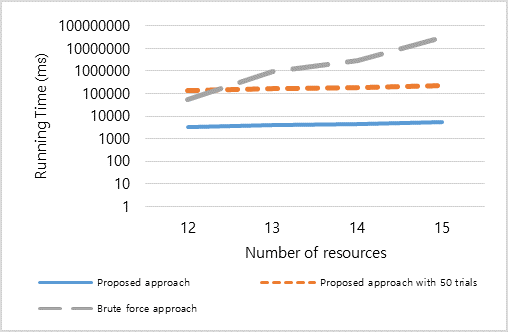
[Figure 6. Running time of the proposed approach]
Figure 6 shows the running time of the proposed approach. The running time with 16 resources was not measured due to the extremely long execution time of the brute force approach. To compare the rapid growth of the running time of the brute force approach against the proposed approach effectively, the values on the y axis of the graph are shown in a log scale. As shown in the figure, an iteration of the proposed approach takes much less time than in the brute force approach. The overall running time of the proposed approach increases linearly as the number of IoT resources increases. The running time of the brute force approach is measured by executing it with a randomly selected input dataset out of the 50 datasets. The running time of the brute force approach exceeds the running time of the proposed approach with 50 trials except for when 12 IoT resources were used.
As the brute force approach traverses every possible solution to find the optimal solution, the running time of the brute force approach increases exponentially with the number of IoT resources. In the worst-case scenario, the number of solutions that the brute force approach must traverse is O(No. of gateways)(No. of IoT resources+No. of gateways). If the numbers of IoT resources and gateways increase, the running time of the brute force approach increases drastically. On the other hand, the proposed approach shows a linear increase in the running time, as the proposed approach performs a fixed number of trials, and the maximum running time of each trial is bound to the number of evolutions done in the genetic algorithm.